2019. 10. 7. 05:46ㆍAlgorithm
참고 : http://egloos.zum.com/incredible/v/4731015
Particle swarm optimization (입자 군집 최적화) [algorithm]
입자 군집 최적화 [알고리듬]Particle swarm optimization (PSO)http://en.wikipedia.org/wiki/Particle_swarm_optimizationhttp://www.swarmintelligence.org/tutorials.phphttp://en.wikipedia.org/wiki/Swarm_intelligence_
egloos.zum.com
https://mamadyonline.github.io/a-tutorial-on-optimization-algorithms-example-of-pso-en.html
A tutorial on optimization algorithms, example of PSO
mamadyonline.github.io
최적화 알고리즘이란?
선택 가능한 해의 집합에서 문제의 최적화를 위해 가장 최고의 해를 찾는 것이다. 최적화 문제는 어디에나 있는데, 예를 들어 마트에 들어가서 필요한 물건을 최소의 금액과 가장 단시간 안에 찾는것을 생각 해 볼 수 있다. 이 경우, 시간과 예산에 대한 최적화가 필요하다.
최적화 문제는 다음 세 가지로 정의 해 볼 수 있다.
-
최대화 하거나 최소화 해야 하는 성공의 측정 (비용 함수, cost function)
-
문제에 대한 가능한 입력사항. (설계변수, design variables) 해당 사항들은 제약사항을 따를 수 있으며 그에따라 탐색할 수있는 영역이 제한되기도 한다.
-
최고의 해를 찾기 위해 탐색할 수 있는 가능한 해결 방법의 집합.
일반적으로 솔루션의 탐색은 시간도 많이 걸리고 매우 무겁다. 그렇기 때문에 이러한 문제를 합리적인 시간안에 적절히 해결하고 수용가능한 해결책을 찾기 위한 다양한 알고리즘이 존재한다.
PSO알고리즘이란?
PSO는 사회적 행동 시뮬레이션을 시도하는 반복적 최적화 알고리즘이다. 1995년 Dr.Eberhart와 Dr.Ennedy가 개발하였다.
단독으로 행동할 때 보다 목표를 달성하기 위해 함께 움직이는 것에 더 잘 작동한다. PSO는 일련의 가능한 후보군들, 개별 입자라고 불리는 정보 공유를 지배함으로써 사회적 행동을 활용한다.
개별 입자는 다음과 같이 정의된다.
-
위치(position). 예를 들어 이차원으로 제한된다면 입자는 (x, y)로 정의될 것이다.
-
속도(velocity). 최적 솔루션을 향해 움직이는데 이용되는 값.
정보 교환은 두 가지 방법으로 이루어지고, PSO의 두 가지 변형된 형태를 제공한다.
-
Local PSO : 정보 공유는 모든 입자들간에, 그리고 직접적으로 연결되는 이웃들 같에 이루어 진다. 매 반복마다 입자들의 움직임은 지역적 최적 위치 (local best known position)에 의해 영향을 받는다. 입자와 그 이웃은 링 데이터 구조 위상(ring data structure topology) 으로 형성되었다.
-
Global PSO: 최적의 위치로 정의된 모든 입자들간의 정보교환이다. 각 반복에서 모든 다른 입자들의 움직임을 안내하는 가장 좋은 위치라고 볼 수 있다. 여기서 입자들은 항성 데이터 구조 위상(star data structure topology)으로 구성되어 있다
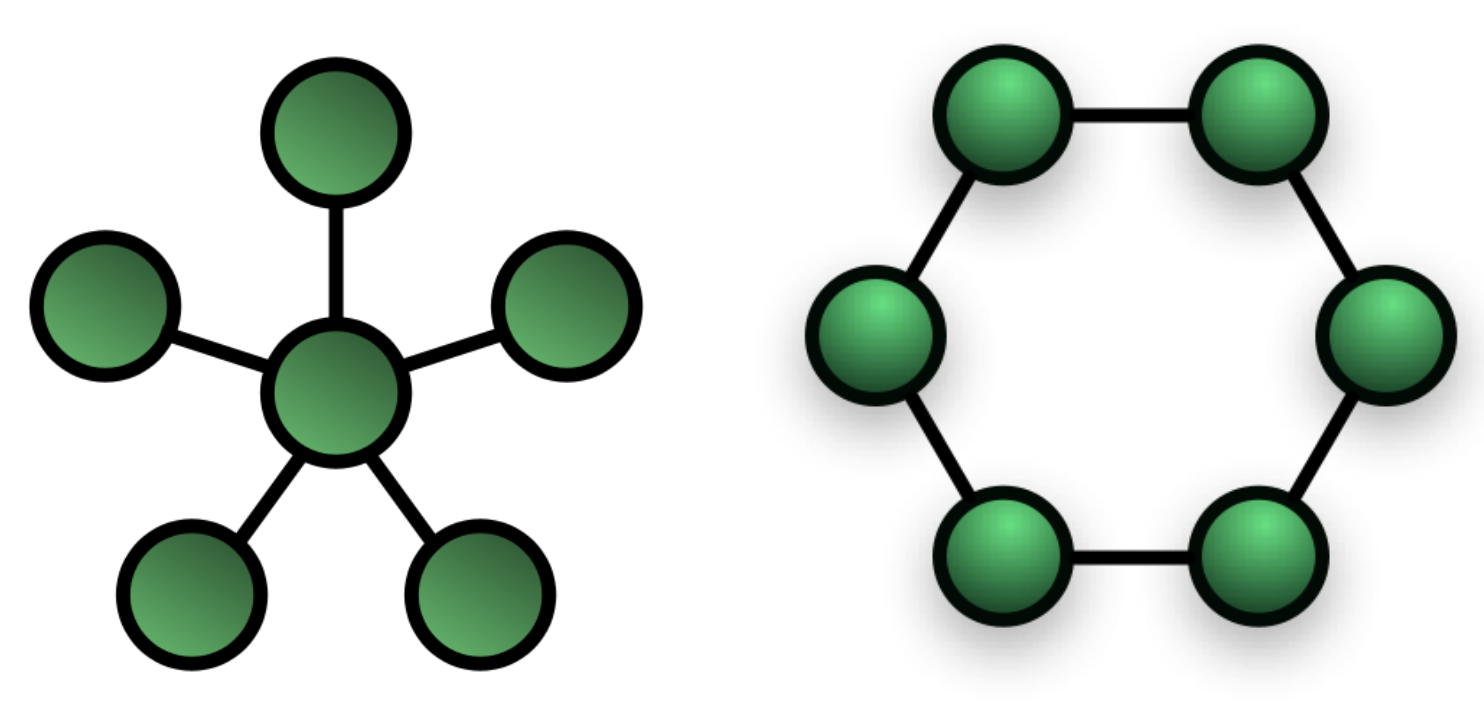
알고리즘
탐색 공간에서 입자 수를 무작위로 초기화 하면서 시작한다. 많은 반복을 통해서 각 입자는 local PSO를 고려하는지, global PSO를 고려하는지에 따라서 각 반복에서 전역 최적해나 이웃들간의 지역회적해를 통한 최적 위치로 향한다.
여기 global PSO의 의사코드 (pseudo-code)가 있다
For 각 입자
입자별 위치(position)와 속도(velocity)를 임의의 값으로 초기화
END
Do
For 각 입자
fitness value 계산 (성공 측정)
If fitness value 가 best fitness value(pBest)보다 낫다면
현재 value를 새로운 pBest로 변경
END
가장 좋은 fitness 값을 가지고 있는 입자를 gBest로 선택
For 각 입자
입자 속도(velocity)계산
계산한 속도를 가지고 입자의 위치(position) 업데이트
End
최대 반복 횟수나 최소 에러 기준에 도달하지 않는 경우 계속 진행
Python 구현
논의해야 할 것은 입자의 position과 velocity의 초기화와 update다.
-
입자는 연속균등분포(uniform distribution)에 따라 랜덤하게 초기화 한다
-
update는 다음 논문에서 약간 수정된 버전으로 수행한다.
import numpy as np
class PSO(object):
"""
Class implementing PSO algorithm
"""
def __init__(self, func, init_pos, n_particles):
"""
Initialize the key variables.
Args:
fun (function): the fitness function to optimize
init_pos(array_like):
n_particles(int): the number of particles of the swarm.
"""
self.func = func
self.n_particles = n_particles
self.init_pos = init_pos
self.particle_dim = len(init_pos)
self.particles_pos = np.random.uniform(size=(n_particles, self.particle_dim)) \
* self.init_pos
self.velocities = np.random.uniform(size=(n_particles, self.particle_dim))
#Initilize the best positions
self.g_best = init_pos
self.p_best = self.particles_pos
def update_position(self, x, v):
"""
Update particle position
Args:
x (array-like): particle current position
v (array-like): particle current velocity
Returns:
The updated position(array-like)
"""
x = np.array(x)
v = np.array(v)
new_x = x + v
return new_x
def update_velocity(self, x, v, p_best, g_best, c0=0.5, c1=1.5, w=0.75):
"""
Update particle velocity
Args:
x(array-like): particle current position
v (array-like): particle current velocity
p_best(array-like): the best position found so far for a particle
g_best(array-like): the best position regarding all the particles found so far
c0 (float): the congnitive scaling constant, 인지 스케일링 상수
c1 (float): the social scaling constant
w (float): the inertia weight, 관성 중량
Returns:
The updated velocity (array-like).
"""
x = np.array(x)
v = np.array(v)
assert x.shape == v.shape, "Position and velocity must have same shape."
# a random number between 0 and 1
r = np.random.uniform()
p_best = np.array(p_best)
g_best = np.array(g_best)
new_v = w*v + c0*r*(p_best - x) + c1*r*(g_best-x)
return new_v
def optimize(self, maxiter=200):
"""
Run the PSO optimization process utill the stoping critera is met.
Cas for minization. The aim is to minimize the cost function
Args:
maxiter (int): the maximum number of iterations before stopping the optimization
Returns:
The best solution found (array-like)
"""
for _ in range(maxiter):
for i in range(self.n_particles):
x = self.particles_pos[i]
v = self.velocities[i]
p_best = self.p_best[i]
self.velocities[i] = self.update_velocity(x, v, p_best, self.g_best)
self.particles_pos[i] = self.update_position(x,v)
# Update the besst position for particle i
if self.func(self.particles_pos[i]) < self.func(p_best):
self.p_best[i] = self.particles_pos[i]
# Update the best position overall
if self.func(self.particles_pos[i]) < self.func(self.g_best):
self.g_best = self.particles_pos[i]
return self.g_best, self.func(self.g_best)
def sphere(x):
"""
In 3D : f(x,y,z) = x² + y² + z²
"""
return np.sum(np.square(x))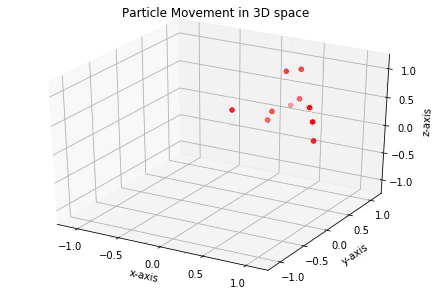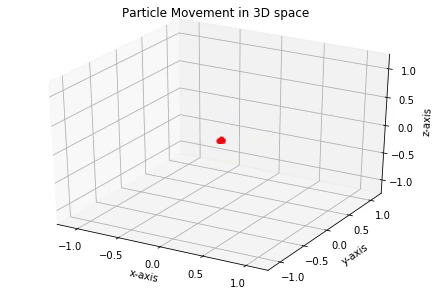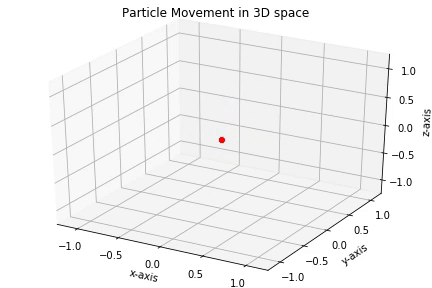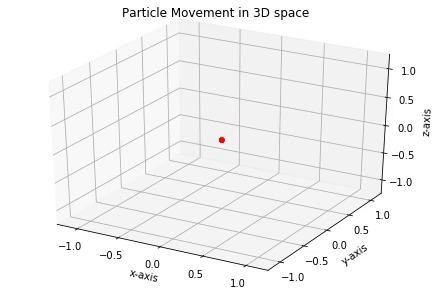
논의해야 할 사항들
1. 초기 위치는 알고리즘을 최적화 할 때 매우 중요하다.
2. PSO는 확률적 알고리즘이다. update와 수행은 랜덤 process를 이용한다. 이로 인해 여러 최적화 프로세스 수행하기 위한 솔루션을 추적하기 어려워질 수 있다. 하지만 항상 random seed를 사용할 수 있다.
3. 완전한 전역 최적 솔루션을 찾아내는 것은 아니다. 하지만 이에 근접하는 것을 잘 찾아낸다.
4. 입자의 수에따라 수렴은 더 오래 걸릴 수 있다. 일반적으로 50개 이상 넘지 않는 것이 좋다.
5. 복잡한 함수에 대해서는 좋은 솔루션을 찾기 전 500회에서 1000회 정도로 좀 더 많은 반복이 필요할 것이다.
좀 더 심회된 PSO를 사용하려면 Pyswarms 라이브러리를 추천한다.
'Algorithm' 카테고리의 다른 글
| Feature Engineering (0) | 2019.10.30 |
|---|---|
| P-value #2/2 (0) | 2019.09.26 |
| P-value # 1/2 (0) | 2019.09.11 |