2021. 1. 2. 15:12ㆍPython
김성 교수님의 Youtube 강의 PyTorchZeroToAll 3강을 참조하였습니다.
Compute Gradient

w의 관점에서 보았을 때 loss의 gradient는 ∂loss/∂w
그렇다면 더 복잡한 모델에서의 Gradient 계산은 어떻게 해야 할까?
Chain Rule
f = f(g), g = g(x) 라고 했을 때, df/dx = df/dg * dg/dx 로 표현할 수 있다.
-
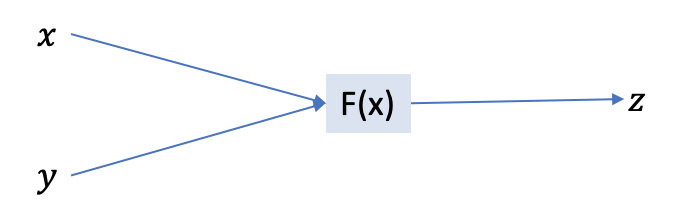
forward pass : x=2, y=3 라고 가정한다.
-
2*3=6. z는 6이다.
-
local gradient을 계산한다.
-
∂z/∂x = ∂xy/∂x = y
-
∂z/∂y = ∂xy/∂y = x
-
-
∂Loss/∂z=5라고 가정했을 때, Backpropagation을 계산해보자.
-
∂Loss/∂x = ∂L/∂z * ∂z/∂x = 5*y = 5*3 = 15
-
∂Loss/∂y = ∂L/∂z * ∂z/∂y = 5*x = 5*2 = 10
-
Computational Graph
Computational Graph로 Backpropagation을 계산 해 보자.
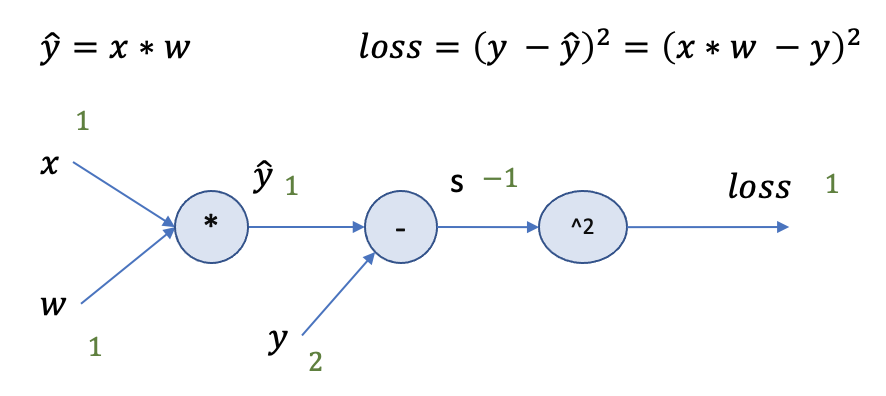
-
x=1, y=2, w=1 인 경우 Forward pass를 진행합니다. yhat=1, yhat-y=-1로 계산할 수 있고 loss는 1로 계산될 수 있다.
-
Backward Propagation을 진행한다. (마지막 연산부터 진행)
-
∂loss/∂s = ∂(s*s)/∂s = 2s = 2*-1 = -2
-
∂(yhat-y)/∂yhat = 1
-
∂loss/∂yhat = ∂loss/∂s * ∂s/∂yhat = -2 * 1 = -2
-
∂(x*w)/∂w = x = 1
-
∂loss/∂w = ∂loss/∂yhat * ∂yhat/∂w = -2 * 1 = -2 ( 계산하고자 하는 gradient)
-
Excercise
-
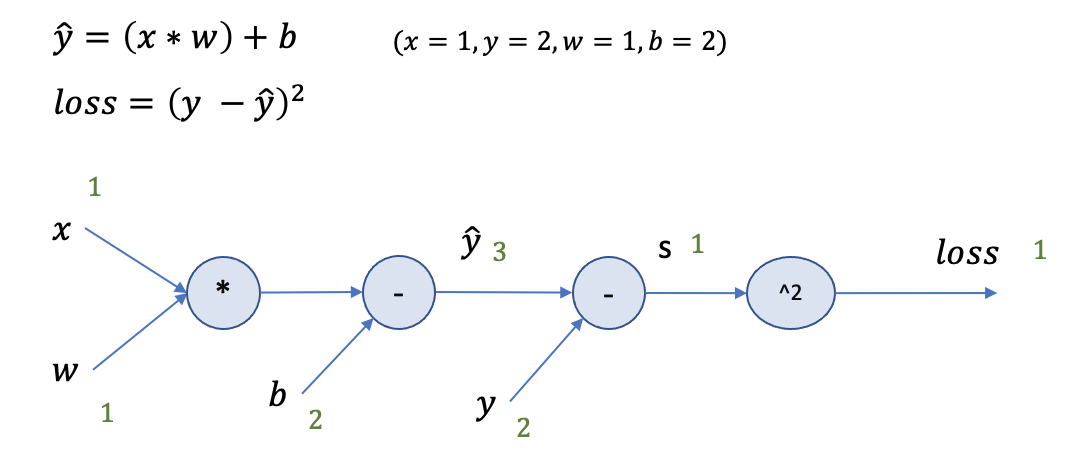
Forward pass
-
Backward Propagation
-
∂(s*s)/∂s = 2s = 2
-
∂s/∂yhat = ∂(yhat - y)/∂yhat = 1
-
∂loss/∂yhat = ∂loss/∂s * ∂s/∂yhat = 2 * 1 = 2
-
∂yhat/∂w = ∂(wx+b)/∂w = x = 1
-
∂loss/∂w = ∂loss/∂yhat * ∂yhat/∂w = 2*1 = 2
-
'Python' 카테고리의 다른 글
| [Pytorch] Wide & Deep (0) | 2021.01.09 |
|---|---|
| [Pytorch] Linear Regression in PyTorch way (0) | 2021.01.03 |
| Jupyterlab Ipywidgets 설치 (Mac, Anaconda) (0) | 2019.12.01 |
| numpy where (0) | 2019.11.10 |